PASATIEMPOS MATEMÁTICOS

Estos son los diferentes acertijos, problemas, pasatiempos, etc. de tipo matemático o lógico, que pusieron a prueba el ingenio de mis alumnos a lo largo de los cursos 

CUESTIÓN 1: EL TRIÁNGULO Y EL HEXÁGONO

«Un triángulo equilátero y un hexágono regular tienen perímetros iguales. Si el triángulo tiene una superficie de 4 unidades cuadradas, ¿qué área tiene el hexágono?»

(Aviso: este problema se puede resolver de una forma un tanto ardua, a base de cálculo; pero también existe una solución muy rápida y elegante, que es la que valoraré. ¡A ver si das con ella!)

Una pista: intenta descomponer el triángulo en otros más pequeños, y compáralos con el hexágono. Parece ser que este problema se os resiste, pero os aseguro que la solución es muy simple... En cualquier caso, si alguien me aporta cualquier otro tipo de solución, será bien recibida...

Solución: 6 u². Enrique González Rodrigo (1º Bachillerato A) ha sido el primero en obtener la solución, de una forma muy brillante (haz clic aquí para ver su solución...). Sin embargo, existe una forma mucho más rápida y elegante -sin necesidad de hacer cálculos-, por triangulación:

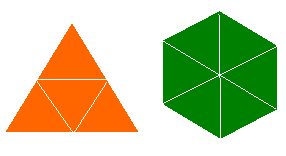
Descomponemos el triángulo en cuatro triángulos equiláteros iguales, como muestra la figura, y lo mismo hacemos con el hexágono, pero esta vez necesitaremos seis triángulos, por cierto idénticos a los anteriores. Por lo tanto, basta contar para ver que, si el área del triángulo es 4 u², la del hexágono será 6 u²

CUESTIÓN 2: EL LORO  (Una cuestión de pura lógica...)

«-Le garantizo-, aseguró a un cliente el dependiente de una pajarería, -que este loro repetirá todo lo que oiga-. El cliente se llevó el loro, pero no consiguió que este dijera ni una palabra. Y, sin embargo, el vendedor había dicho la verdad. ¿Cómo puedes explicarlo?»

Solución: César Cuevas Lara (1º Bachillerato A) ha dado con la solución que, una vez obtenida, resulta lógica y evidente: ¡el loro era sordo!

CUESTIÓN 3: LOS DOS BARBEROS  (Otra cuestión de lógica)

«Un lógico, de paso por una pequeña localidad, decidió cortarse el pelo. Había en la villa solamente dos peluquerías. Tras echar un vistazo a una de ellas, la vio extraordinariamente descuidada. Además, su dueño llevaba el pelo lleno de trasquilones. La otra barbería era un ejemplo de pulcritud. Su barbero estaba recién afeitado, su vestimenta era impecable, y presentaba un peinado perfecto. El lógico decidió ir a cortarse el pelo en la primera. ¿Por qué?»

Solución: María Padilla y Luz Alcolea (1º Bachillerato A) han llegado al mismo tiempo a la resolución del problema que, de nuevo, una vez vista resulta obvia: para hacerse cortar el pelo, cada barbero tiene que recurrir a los servicios del otro. El lógico eligió al barbero que mejor había arreglado el pelo a su competidor.

CUESTIÓN 4: LAS TRES HIJAS

«Dos profesores de Matemáticas que están charlando sobre sus respectivas familias sostienen el siguiente diálogo:
- Por cierto, ¿de qué edad son tus tres hijas?
- El producto de sus edades es 36.

- Para averiguar sus edades necesito más datos...

- Su suma casualmente es igual al número de tu casa.
  Tras reflexionar un rato, el que ha formulado la pregunta dice:
- Me falta un dato.
- Tienes razón - admite el otro - Me había olvidado que mi hija mayor toca el piano.
¿Qué edades tienen las tres hijas del profesor?»

Solución: Irina Bredykhina (1º Bach. B) ha dado, por fin, con la clave: se trata de formar todos los posibles tríos cuyo producto sea 36:

 1  1  36

 1  2  18

 1  3  12

1  4   9

                 1  6   6   suman  13

                 2  2   9  suman 13

2  3   6

3  3   4

Como veis, hay dos posibilidades que suman igual (13, en concreto); para ver cuál de las dos es la correcta, faltaba el dato de que existe una hija mayor (es decir, no pueden ser las dos hijas mayores de 6 años...). ¡Lógico!, ¿verdad?.

CUESTIÓN 5: LA PIEZA METÁLICA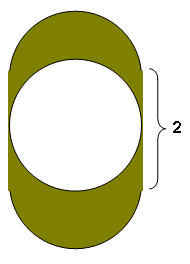 

«A una chapa metálica, formada por un cuadrado de dos metros de lado rematado por dos semicírculos adosados en sus lados opuestos, se le practica en su centro un corte circular de dos metros, como indica la figura. ¿Qué superficie tendrá la pieza resultante? »

(Aviso: este problema también se puede resolver de una forma laboriosa, a base de cálculo, pero existe una solución muy rápida, que es la que valoraré más. ¡Es muy sencilla!)

Solución: 4 m²; Luz Alcolea (1º Bachillerato A) ha sido la primera en darse cuenta de que si trasladamos las dos semicircunferencias exteriores hasta el centro de la figura, entonces rellenan el círculo central, con lo que la chapa pasa a ser un cuadrado de lado 2m.

CUESTIÓN 6: LA FUENTE  (Otro de geometría aplicada a la vida misma...)

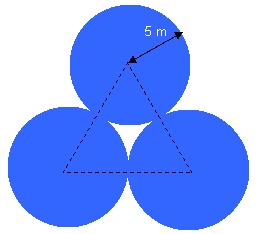
«Un ayuntamiento proyecta construir una fuente como la que indica la figura. Si su profundidad es de un metro, ¿cuántos litros de agua cabrán?»

Solución: Pedro Jesús León (4º ESO A) y Zaur Gussalov (1º Bachillerato B) han llegado prácticamente al mismo tiempo a la solución. Haz clic en cualquiera de sus nombres para verla. La idea es que hay que tener en cuenta el área de la pequeña figura triangular central...

CUESTIÓN 7: FUMAR PERJUDICA SERIAMENTE LA SALUD 

«Un fumador tiene 215 puros repartidos en paquetes de 3, 6 y 8 puros. Con grave riesgo para su salud, se fuma todos los paquetes de 6 puros y un número igual de paquetes de los de 3. En el resto de paquetes de 3 se fuma dos puros, de manera que queda uno en cada paquete. Los de 8 están intactos. En un momento dado comprueba que le quedan 85 puros en total. ¿Cuántos paquetes tenía de cada clase?»

(Una pista: llamad x al nº de cajas de puros de 3 que tenía al principio, y al de 6, y z al de 8, y plantead todas las posibles soluciones posibles, es decir, números enteros positivos, descartando las imposibles...)

Solución: Enrique González (1º Bach. A) y Celia Mena (1º Bach. B) (haz clic en sus nombres)

CUESTIÓN 8: LAS CHULETAS  (Un problema de lógica práctica)

«Supongamos que disponemos de una parrilla pequeña, en la que sólo caben dos chuletas, y en la que queremos asar tres chuletas en el mínimo tiempo posible. Supongamos también que hacen falta 20 minutos para asar una chuleta por los dos lados (10 por cada lado). A primera vista, y como sólo podemos asar dos a la vez, en 20 minutos tendremos listas las dos primeras, y la tercera tardará otros 20, con lo cual habremos invertido 40 minutos. Sin embargo, existe una forma de ahorrarse 10 minutos. ¡Encuéntrala!»

Solución: Esta vez la cosa ha estado repartida: Fran Santos (4º ESO A), Sheila Medina (1º Bach. A) y Fran López Vallejo (1º Bach. A) han dado con la solución. Haz clic en cualquiera de sus nombres para verla. Si llamamos A, B y C a las chuletas, cada una con lados 1 y 2, la idea es asar los lados A1 y B1 en los primeros 10 minutos, y retirar una de ellas, por ejemplo B. En los 10 minutos siguientes asamos A2 y C1, con lo que A ya estará terminada. Finalmente, en los últimos 10 minutos asaremos B2 y C2.

CUESTIÓN 9: LAS VASIJAS

«Una persona necesita sacar de un depósito 7 litros de agua. Dispone para ello únicamente de dos vasijas, de 9 y 4 litros respectivamente. ¿Cómo tiene que proceder?»

Solución: Zaur Gussalov, un asiduo, (1º Bach. B) y Octavio José Requena (1º Bach. B) han dado con ella: llenamos la vasija de 4 l  y la vertemos en la de 9 l dos veces, con lo cual tendremos 8 l en ésta última; llenamos de nuevo la de 4 l y la vertemos en la de 9 l hasta llenarla, con lo que nos quedarán 3 l en la de 4 l; vaciamos la de 9 l y vertemos los 3 l en ella; finalmente, llenamos la de 4 l y la vertemos en la de 9 l. ¡Fácil!

CUESTIÓN 10: OTRO DE BARBEROS

«En un pueblo hay hombres solteros, casados y viudos. De ellos, algunos son imberbes y otros tienen barba. Además, algunos se afeitan ellos mismos y otros acuden al único barbero del pueblo.

Por otra parte, en el pueblo existen tres razas: negros, blancos y mestizos.

Sabiendo que:

- El barbero tiene bigote.

- El barbero afeita sólo a los viudos y solteros, no blancos en ambos casos.

- Sólo se afeitan a sí mismo todos los que no son negros y son solteros.

, ¿serías capaz de decir la raza y estado civil del barbero?»

Solución: María Padilla Díaz ha encontrado la clave: el barbero es mestizo y soltero. En efecto:

1. La 1ª condición nos dice que el barbero tiene bigote, por lo cual no es imberbe, es decir, tendrá o puede tener barba, pero en cualquier caso necesitará afeitarse. Ahora bien, como él es el barbero del pueblo, se tendrá que afeitar a sí mismo.
2. La 2ª condición nos dice que el barbero afeita sólo a los viudos no blancos y a los solteros no blancos; por lo tanto, afeita a las siguientes cuatro categorías: los viudos mestizos, los viudos negros, los solteros mestizos y los solteros negros.
3. Ahora bien, como antes vimos que se afeitaba a sí mismo, la 3ª condición nos hace ver que el barbero no puede ser negro y tiene que ser soltero. Viendo las cuatro categorías anteriores, la única válida es que el barbero sea soltero y mestizo. ¡Pura lógica!

CUESTIÓN 11: CRIPTOGRAMA (Propuesto por Enrique González, 1º Bach. A)

Cada letra corresponde a un número y letras diferentes corresponden a números diferentes. Encuentra A, B y C:

A  B  C

       A  B  C     +

A  B  C

B  B  B

Solución: Zaur Gussalov (1º Bach. B), ¡cómo no!, ha obtenido A=1, B=4 y C=8, ya que:

1  4  8

       1  4  8     +

1  4  8

4  4  4

CUESTIÓN 12: UNO DE GEOMETRÍA (¡Parece que se os resiste!)

«En la figura se muestran cuatro círculos de radio 1 dentro de un círculo mayor. ¿Cuál es el área sombreada? (No utilices decimales: indica la solución en función de raíces y de π)»

Solución: Pedro Jesús León (4º ESO A) ha dado, por fin, con la clave. Haz clic en su nombre para ver su brillante solución.

CUESTIÓN 13: LA CUERDA DE LA FERIA

«Un tratante de ganado tenía 32 ovejas dispuestas en ocho corrales de planta cuadrada. En cada corral de las esquinas hay una oveja y en cada uno de los centrales hay siete, de acuerdo con la siguiente disposición:

1	7	1
7		7
1	7	1

El tratante cuenta cada noche las ovejas que hay en cada hilera y se asegura de que sean nueve. Una vez hecho esto, se retira a dormir. Cierto día le roban cuatro animales. Cuando el tratante hace su recuento nocturno no se percata de nada, pues las ovejas siguen sumando nueve por hilera. ¿Qué hicieron los ladrones para burlar al tratante? ¿Cómo situaron en los corrales a las ovejas que dejaron?

Tres días más tarde le roban otras cuatro y tampoco el tratante se dio cuenta de nada al contar. ¿Cómo lo volvieron a burlar?

Una semana después, el tratante realizó su habitual recuento, le salieron las cuentas, y volvió tranquilo a dormir. Pero, a la mañana siguiente, una inspección del veterinario descubrió que sólo quedaban 20 ovejas. ¿Qué hicieron los ladrones para burlar por tercera vez al ingenuo tratante? ¿Hubiera sido posible un cuarto robo?»

Solución: Enrique González Rodrigo (1º Bach. B) ha encontrado la solución:

Los ladrones pasan una oveja del centro de cada hilera a un lateral:

2	6	2
6		6
2	6	2

y pueden robar, entonces, una oveja del centro de cada hilera -es decir, cuatro ovejas en total-, ya que cada hilera seguirá sumando 9:

2	5	2
5		5
2	5	2

Y así, de la misma forma, pueden efectuar otro robo:

3	4	3
4		4
3	4	3

3	3	3
3		3
3	3	3

Todavía pueden cometer un último robo:

4	2	4
2		2
4	2	4

4	1	4
1		1
4	1	4

Obviamente, no pueden efectuar más robos, ya que no es posible quitar una oveja de cada centro y dejar cada hilera con 9 ovejas:

5		5
5		5

CUESTIÓN 14: LA BRUJITA MÁGICA

Haz clic aquí para acceder a una curiosa presentación que me han enviado. (Para volver aquí, tendrás que dar al botón de retroceso de tu navegador). ¿Increíble, verdad?. Pues la explicación es bastante sencilla. ¿Serías capaz de descubrirla?

Solución: Mónica Díaz Sobrino y Víctor León Olmo (4º ESO C) han dado con ella conjuntamente. La cosa, una vez vista, es muy simple: si designamos el número de dos cifras que elegimos como ab (p. ej. 75), entonces se puede escribir en forma polinómica como 10a+b (en el ejemplo anterior, 75=7·10+5); por lo tanto, si le restamos la suma de sus cifras, quedará:

10a+b-(a+b)=10a+b-a-b=9a

es decir, escojamos el número que escojamos, si le restamos la suma de sus cifras siempre resultará múltiplo de 9. Lo que hace la brujita es asignar a los múltiplos de 9 siempre el mismo signo (y, para disimular, cambia la cuadrícula en cada visita pero, eso sí, asignando a todos los múltiplos de 9 el mismo signo). Fácil, ¿no?.

CUESTIÓN 15: LAS CERILLAS

Este es un acertijo muy viejo, pero no me resisto a proponerlo, porque nos enseña que en muchas circunstancias de la vida no hay que obsesionarse con una sola forma de ver las cosas, sino más bien estar abierto a otras posibilidades. «¿Cómo podríamos formar, con seis cerillas iguales, exactamente cuatro triángulos equiláteros?»

Solución: Confieso que cometí un pequeño error en el enunciado, ya que debí añadir que había que aprovechar la totalidad de la longitud de cada cerilla. Si no, el asunto es bastante fácil, dándose varias soluciones triviales, como la que ha descubierto Víctor León Olmo (4º ESO C):

Pero si imponemos que se utilice la totalidad de la longitud de cada cerilla, entonces no hay soluciones en el plano. Hay que ser imaginativos y caer en la cuenta de que la solución está ¡en el espacio!:

es decir, un tetraedro. A ello han llegado Ángel Domingo Perea (2º Bach. A) y Alba Domingo Perea (4º ESO C).

CUESTIÓN 16: LAS TRES GORRAS

Un problema de lógica: «Un juez escoge tres gorras de un conjunto de tres blancas y dos negras. Tres personas sentadas, alineadas una tras otra, y todas mirando de frente (de forma que cada una sólo puede ver la gorra de los que tiene delante) cierran los ojos mientras se les coloca su gorra. Las gorras no utilizadas se ocultan a la vista. El juez le pregunta al último de la fila si sabe el color de su gorra, y éste contesta: "No lo sé". El del centro contesta lo mismo. Finalmente, el situado delante contesta con total seguridad: "Mi gorra es blanca". ¿Cómo pudo deducirlo?»

Solución: La han encontrado María Chicharro (4º ESO C) y Enrique González Rodrigo (2º Bachillerato A) -éste último, un habitual en esta sección-. Recordar que hay tres gorras blancas, que llamaremos B B B, y dos negras, N N. En primer lugar habla el último de la fila, el que ve a los otros dos de delante, que contesta que no sabe el color de la gorra que lleva. Eso significa que tenemos que descartar el siguiente caso:

	delante:	N
Disponibles: B B B N N	centro:	N
	último:	?

pues, en ese, caso, hubiera respondido lógicamente que su gorra es B. Por lo tanto, independientemente de la gorra que lleve el 1º, los dos de delante sólo pueden llevar, en principio, alguna de las tres posibilidades siguientes:

	1	2	3
último:	B	B	N
centro:	B	N	B
primero:	?	?	?

Esto lo tiene en cuenta el del centro, que contesta que tampoco sabe el color de su gorra. Por lo tanto, la gorra que ve delante de él no puede ser N, porque entonces él concluiría que estamos en la posibilidad 3 y contestaría que su gorra es B. Por consiguiente, sólo quedan dos posibilidades, y en ambas la gorra es B.

CUESTIÓN 17: CURIOSA PROPIEDAD

«Los números 48 y 42 tiene una extraña propiedad: su producto no se altera aunque cambiemos de orden las cifras que los componen:

48·42=84·24

¿Hay otros números de dos cifras con la misma propiedad? En caso afirmativo, ¿podrías deducir razonadamente una regla general?»

Solución: Jesús Ortiz Molina (4º ESO C) ha advertido la condición que deben cumplir dos números de dos cifras, ab y cd, para que

ab·cd=ba·dc

No era muy difícil observar que tal condición es que a·c=b·d, es decir, que el producto de las decenas es igual al de las unidades, lo cual ha observado con varios ejemplos, incluido el que yo proponía:

48·42=84·24 ya que 4·4=8·2

24·21=42·12  ya que 2·2=4·1

68·43=86·34 ya que 6·4=8·3

etc...

Ahora bien, en Matemáticas no basta con esto; además, hay que razonarlo. Quiero decir que es posible que esto se cumpla para muchos ejemplos, pero, ¿hasta qué punto podemos estar seguros de que se cumple siempre? Sí, ya sé que la intuición nos dice que esto va a ser siempre así. Pero la experiencia, y las Matemáticas, nos dicen que la intuición muchas veces puede fallar. Vamos a probar que se cumple siempre. La idea es volver a aplicar la descomposición polinómica de un número, ya utilizada en las cuestiones 14 y 22. En efecto, la expresión

ab·cd=ba·dc

se puede descomponer polinómicamente así:

(10a+b)(10c+d)=(10b+a)(10d+c)

y, operando:

100ac+10ad+10bc+bd=100bd+10bc+10ad+ac

Suprimiendo términos repetidos en ambos miembros, y simplificando, obtenemos la condición buscada:

99ac=99bd

ac=bd

CUESTIÓN 18: EL CAJERO AUTOMÁTICO

«Unos desaprensivos colocan una cámara camuflada en un cajero automático para poder ver qué número secreto (de 4 dígitos) teclea el usuario, para así poder acceder a su cuenta. Para prevenir estas eventualidades, los bancos recomiendan que tecleemos tapando con la otra mano. Supongamos que lo que hace un determinado cliente es, simplemente, situar sus dedos sobre las teclas del 1, 7 y 9, y marcar con estas cifras su número secreto de 4 dígitos, de forma que los cacos no pueden ver en qué orden ha tecleado cada dígito. Averigua cuántos intentos tendrán que hacer, como máximo, los cacos para poder acceder a la cuenta de dicho cliente»

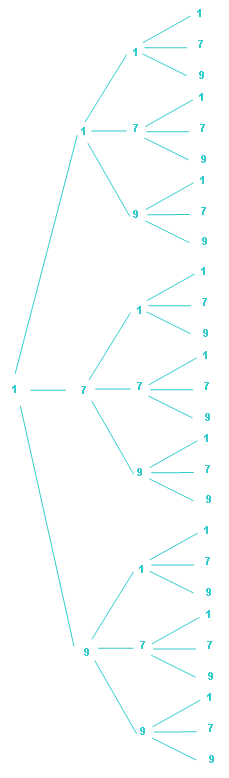Solución: Francisco José Sánchez Lara (4º ESO D) ha encontrado la solución, a base de escribir todas y cada una de las posibilidades de números de cuatro cifras que se pueden formar utilizando solamente el 1, el 7 y el 9. Resultan ser 81 posibles números secretos. Ahora bien, yo voy a razonar por qué son 81 posibilidades, sin necesidad de formarlas todas. ¡Para eso están las Matemáticas, para ahorrarnos ese trabajo!. Para ello, utilizaremos un árbol.

El 81 viene de 3⁴. En efecto, en el árbol adjunto podemos ver todas las posibilidades si comenzamos tecleando un 1. Como 2º número podemos elegir entre 1, 7 o 9, es decir, 3 posibilidades. A su vez, de cada una de estas 3 posibilidades parten otras tres ramas (3^er número a teclear) y, lo mismo ocurre para la 4^a y última cifra del número secreto. Por lo tanto, serían:

1x3x3x3=3³ posibles números, comenzando por 1

Finalmente, dado que el número secreto también puede empezar por 7 o por 9, habría que multiplicar lo anterior por 3 (es decir, podríamos hacer otros dos árboles como el anterior, uno comenzando por 7, y el otro por 9), obteniéndose 3⁴=81 posibles números secretos diferentes.

CUESTIÓN 19: LAS MATRÍCULAS

«Una ciudad, que tiene que implantar un nuevo sistema de matriculación de vehículos, baraja los dos siguientes sistemas: dos letras y tres dígitos decimales, o tres letras y dos dígitos. En ambos casos, para cada letra se dispone de 20 letras diferentes. ¿Con cuál de los dos sistemas se podrán matricular más coches?»

Solución: ¡Por fin alguien ha dado con la solución! Y eso que era muy fácil. En concreto, ha sido Pedro Montero(4º ESO C):

1^er sistema (BZ 152): Por cada una de las 20 posibles letras para la 1ª letra hay otras 20 posibilidades para la 2ª letra, es decir, 20x20. Y por cada una de éstas, hay 10 dígitos para el 1^er número; y, de la misma forma, por cada una de las posibilidades anteriores, hay otras 10 para el 2º dígito, y de la misma forma otras 10 posibilidades para el 3^er dígito. En total:

20x20x10x10x10=400 000 matrículas diferentes posibles

2º sistema (BDC 35): Razonando de la misma forma, las posibilidades, en total, son:

20x20x20x10x10=800 000 matrículas diferentes posibles

es decir, que con el segundo sistema (BDC 35) se podrán matricular más coches -concretamente el doble- que con el primero (BZ 152).

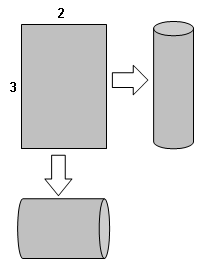
CUESTIÓN 21: LA LATA DE CONSERVAS

Un problema de Geometría de aplicación a la vida real: «En una empresa disponen de láminas metálicas rectangulares en las que la proporción de su lados es de 2 a 3. Desean diseñar con ellas latas de conservas cilíndricas, obviamente de la mayor capacidad posible. ¿Cuál de las dos posibilidades será la elegida?»

CUESTIÓN 22: UNA CURIOSA COINCIDENCIA

«Prueba con varias personas el siguiente juego: "Si sumamos las dos últimas cifras del año en que nacimos a la edad que cumpliremos este año, siempre obtenemos el mismo número". ¿Sabrías explicar el porqué? (NOTA: Sólo funciona para nacidos en el siglo XX)»

Solución: Marta Sánchez Gento (4º ESO D) me ha dado una explicación, si no completa, sí bastante cercana a la solución. Yo voy a dar aquí la explicación rigurosa, que se basa en la descomposición polinómica de un número, que se estudia, creo, en 6º de Primaria y/o en 1º de ESO:

Supongamos que una persona ha nacido en 19ab (por ejemplo, 1995); entonces, la descomposición polinómica de su año de nacimiento sería:

19ab=1900+10a+b

(En el ejemplo citado, 1995=1900+90+5). Por otra parte, la edad de una persona se obtiene, como sabemos, restando al presente año su fecha de nacimiento:

2011-(1900+10a+b)

El enunciado nos dice que sumemos a la edad de la persona, que viene dada por la expresión anterior, las dos últimas cifras de su año de nacimiento, es decir, ab=10a+b:

10a+b+[2011-(1900+10a+b)]

Quitamos paréntesis y simplificamos:

10a+b+2011-1900-10a-b=2011-1900=111

Es decir, ¡obtenemos siempre 111!.

CUESTIÓN 24: EL CICLISTA

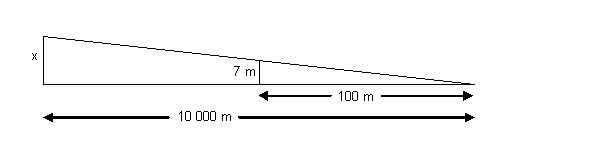
«Cuando una señal de tráfico indica que la pendiente de una carretera es p. ej. del 10 %, quiere decir que por cada 100 m de trayecto horizontal la carretera asciende 10 m. Supongamos que ascendemos por una carretera de montaña cuya pendiente media es del 7 % durante 10 km. ¿Cuánto hemos ganado en altitud?»

 Solución: Alba Moya Martínez (4º ESO C) ha dado con ella. Se trata de aplicar una sencilla regla de tres, o, lo que es lo mismo, aplicar el teorema de Tales (el dibujo adjunto no está a escala):

CUESTIÓN 27: LA EDAD DE DIOFANTO

«Nada se sabe de la vida del matemático griego Diofanto (siglo III d.C.), excepto su edad al morir. Ésta se sabe por una cuestión planteada en una colección de problemas del siglo V o VI, que reza así: "La juventud de Diofanto duró 1/6 de su vida… se dejó barba después de 1/12 más. Después de 1/7 de su vida se casó. Cinco años después tuvo un hijo. Éste vivió exactamente la mitad de tiempo que su padre, y Diofanto murió cuatro años después". Halla la edad de Diofanto»

Solución: Fran López Aguado (4º ESO A) ha sido el primero en dar con ella: Diofanto murió a los 84 años; lo más lógico es traducir el enunciado a una ecuación. Haz clic aquí  para verla.